Welcome to jumble! This program was written as a companion to academic work performed by researchers at Brown University to conduct re-randomization for cluster-randomized nursing home trials.

Introduction

In this vignette we demonstrate some functions used for random assignment, following best practices outlined by other R packages like randomizeR, randomizr etc.

Randomization must be transparent
Randomization must be reproducibile
Randomization must be random!

Example dataset

The example dataset used in this package is freely available and comes from a clinical HIV therapy trial conducted in the 1990s.(Hammer SM 1996) See: ?jumble::ACTG175

Load dataset

df <- jumble::ACTG175

A note on random number generation

The random sampling method underlying jumble functions is the base R function sample(), rbinom(). While computational speed may be problematic in some cases, the base sample function is reliable, stable, and well-documented and tested.

The sample() functions calls the default Random number generator for R, the Mershene-Twister method, which can be queried using RNGKind().@Mersenne1998

Current system build:

## R version 3.6.1 (2019-07-05)

## Windows platform : x86_64-w64-mingw32/x64 (64-bit)

Random assignment to K-groups

Assigning treatment is easy if you want equal probability of assignment to one or more groups, without concern to final sample size in each arm, covariate balance etc.

assign <- rnd_assign(df$pidnum, 2, as.integer(as.Date('2019-06-26')))

head(assign)

## # A tibble: 6 x 2
##      id group
##   <int> <chr>
## 1 10124 a    
## 2 10140 b    
## 3 10165 b    
## 4 10190 a    
## 5 10229 a    
## 6 10361 a

Truly random assignment!

The seed is stored as a attribute

seed_iter <- attr(assign, 'seed')

## [1] "Randomization performed: 2020-01-06 Seed: 18073"

Don’t lose that information! As long as you know the seed you can reproduce the randomization:

assign <- rnd_assign(df$pidnum, 2, seed_iter)

head(assign)

## # A tibble: 6 x 2
##      id group
##   <int> <chr>
## 1 10124 a    
## 2 10140 b    
## 3 10165 b    
## 4 10190 a    
## 5 10229 a    
## 6 10361 a

Simulation to demonstrate equal probability

Perform 20,000 randomizations

pidnum <- df$pidnum  

n=20000L

df_assign <- lapply(1:n, function(x) rnd_assign(pidnum, 2, 18073L+x))

assigns <- bind_cols(df_assign[[1]][, 1], 
                     lapply(df_assign, function(x) x[, 2]))

df_assign_2 <- gather(assigns, key = 'trial', value = 'group', 
                      starts_with('group')) %>%
  group_by(id) %>%
  summarize(`No. of trials` = n,
            `No. group 'a'` = sum(group == 'a'),
            `No. group 'b'` = sum(group == 'b'),
            `Prob. group = 'a'` = `No. group 'a'` / n(),
            `Prob. group = 'b'` = `No. group 'b'` / n())

head(df_assign_2)

## # A tibble: 6 x 6
##      id `No. of trials` `No. group 'a'` `No. group 'b'` `Prob. group = …
##   <int>           <int>           <int>           <int>            <dbl>
## 1 10124           20000            9986           10014            0.499
## 2 10140           20000           10000           10000            0.5  
## 3 10165           20000            9997           10003            0.500
## 4 10190           20000           10003            9997            0.500
## 5 10229           20000            9997           10003            0.500
## 6 10361           20000           10001            9999            0.500
## # … with 1 more variable: `Prob. group = 'b'` <dbl>

First glance shows ~ equal likelihood of group assignment in 20,000 trials. ### Assignment tests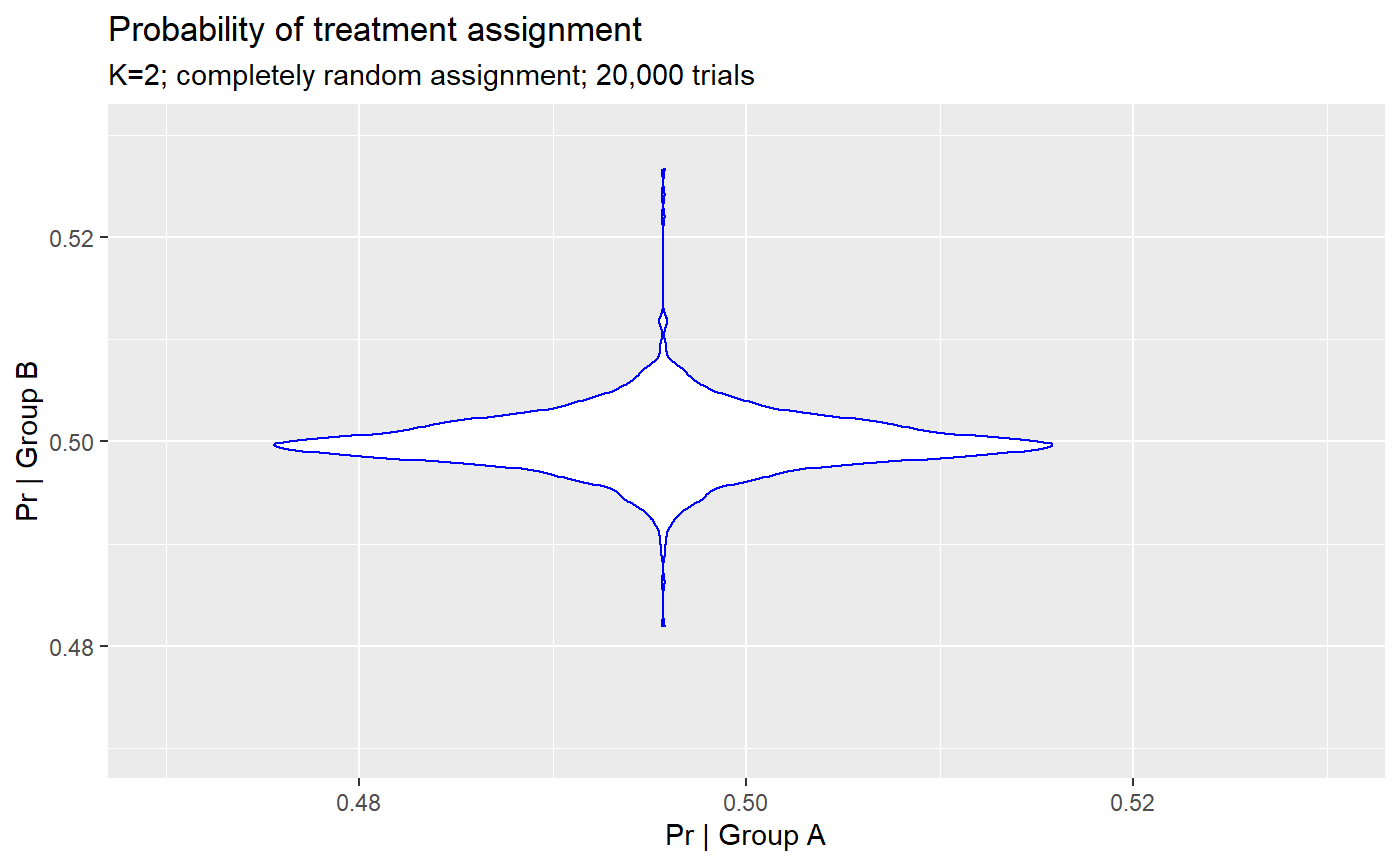

For any given individual, across 20,000 trials no assignment exceeds an imbalance of ~2-3%.

## Probability of assignment to group 'a' in 20,000 trials

##    Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
##  0.4733  0.4984  0.5001  0.5000  0.5015  0.5181

## Probability of assignment to group 'b' in 20,000 trials

##    Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
##  0.4819  0.4985  0.4999  0.5000  0.5016  0.5266

However, in each trial the number of individuals in group A vs. B was random and could be imbalanced.

df_trials <- gather(assigns, key = 'trial', value = 'group', 
                      starts_with('group')) %>%
  group_by(trial) %>%
  summarize(`No. group 'a'` = sum(group == 'a'),
            `No. group 'b'` = sum(group == 'b'))

## No. assigned to group 'a' in 20,000 trials

##    Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
##   459.0   516.0   527.0   526.9   538.0   588.0

## No assigned to group 'b' in 20,000 trials

##    Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
##   466.0   516.0   527.0   527.1   538.0   595.0

See how the number assigned varies widely?

what if you want to guarantee an equal number of individuals are in each group?

Random assignment to K-groups, equal sample size

We will repeat the exercise, dropping one person to make an odd-numbered cohort.

pidnum <- df$pidnum 
pidnum <- pidnum[2:length(pidnum)] # drop 1 

n=10000

seeds <- sample(-100000:100000, n)
df_assign <- lapply(1:n, function(x) {
  set.seed(seeds[x])
  rnd_allot(pidnum)
  })

assigns <- bind_cols(df_assign[[1]][, 1], 
                     lapply(df_assign, function(x) x[, 2]))

df_assign_2 <- gather(assigns, key = 'trial', value = 'group', 
                      starts_with('group')) %>%
  group_by(id) %>%
  summarize(`No. of trials` = n,
            `No. group 'a'` = sum(group == 'a'),
            `No. group 'b'` = sum(group == 'b'),
            `Prob. group = 'a'` = `No. group 'a'` / n(),
            `Prob. group = 'b'` = `No. group 'b'` / n())

head(df_assign_2)

## # A tibble: 6 x 6
##      id `No. of trials` `No. group 'a'` `No. group 'b'` `Prob. group = …
##   <int>           <dbl>           <int>           <int>            <dbl>
## 1 10140           10000            4958            5042            0.496
## 2 10165           10000            4955            5045            0.496
## 3 10190           10000            5026            4974            0.503
## 4 10229           10000            4959            5041            0.496
## 5 10361           10000            4971            5029            0.497
## 6 10368           10000            4943            5057            0.494
## # … with 1 more variable: `Prob. group = 'b'` <dbl>

Assignment tests

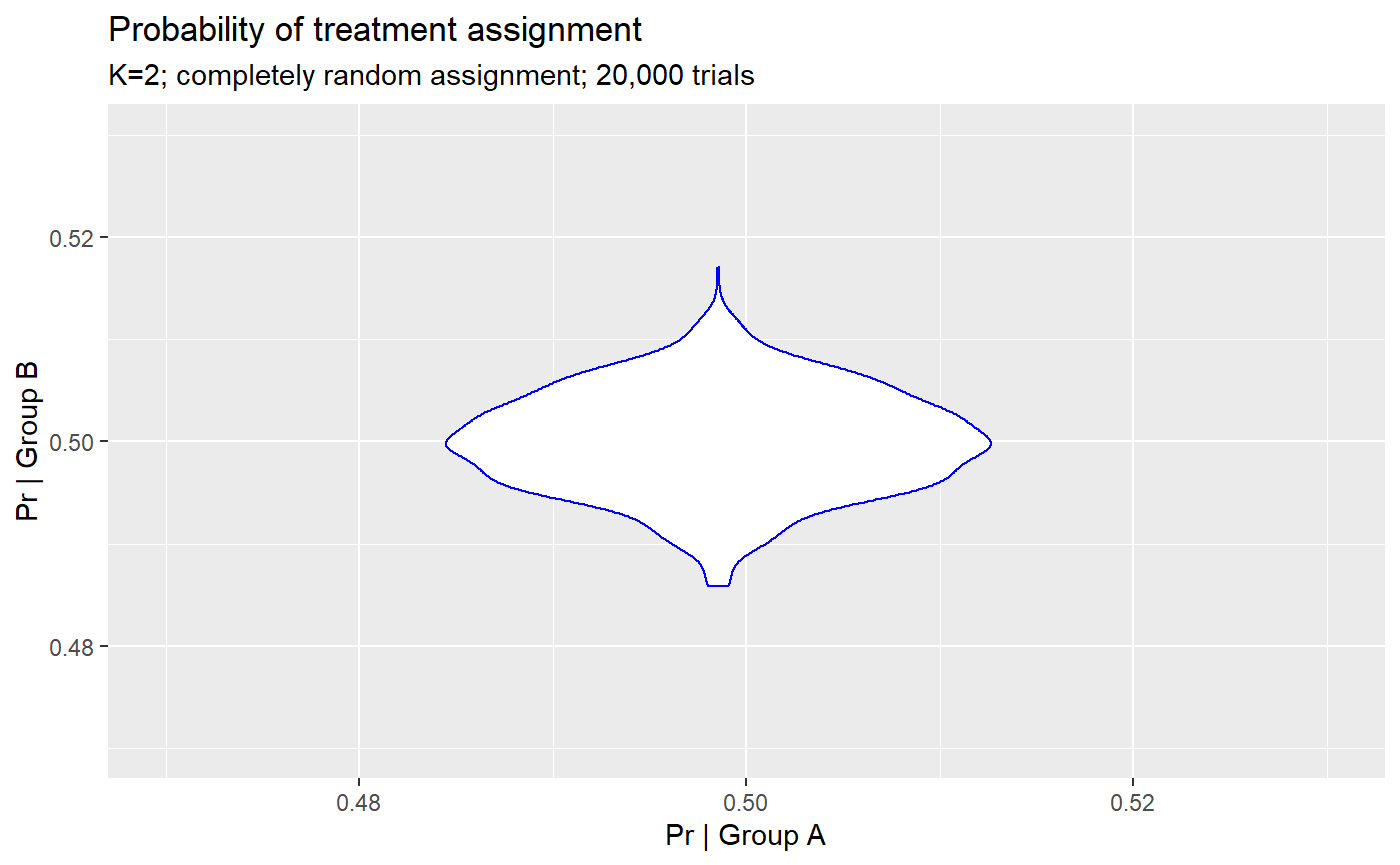
Random assignment looks well-balanced between groups.

## Probability of assignment to group 'a' in 20,000 trials

##    Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
##  0.4829  0.4965  0.5001  0.5000  0.5035  0.5142

## Probability of assignment to group 'b' in 20,000 trials

##    Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
##  0.4858  0.4965  0.4999  0.5000  0.5035  0.5171

df_trials <- gather(assigns, key = 'trial', value = 'group', 
                      starts_with('group')) %>%
  group_by(trial) %>%
  summarize(`No. group 'a'` = sum(group == 'a'),
            `No. group 'b'` = sum(group == 'b'))

What about the size of the groups?

## No. assigned to group 'a' in 20,000 trials

##    Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
##   526.0   526.0   526.0   526.5   527.0   527.0

## No assigned to group 'b' in 20,000 trials

##    Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
##   526.0   526.0   527.0   526.5   527.0   527.0

Equal size! The number now randomly goes between 526 or 527 for either the ‘a’ or ‘b’ group. The imbalance is selected with equal probability.

Contacting authors

The primary author of the package was Kevin W. McConeghy. See here

References

Hammer SM, et al. 1996. “A Trial Comparing Nucleoside Monotherapy with Combination Therapy in Hiv-Infected Adults with Cd4 Cell Counts from 200 to 500 Per Cubic Millimeter.” N Eng J M 335: 1081–90.

jumble: Random assignment

Kevin W. McConeghy

2020-01-06